1.1.1 Tennis Ball Sphere
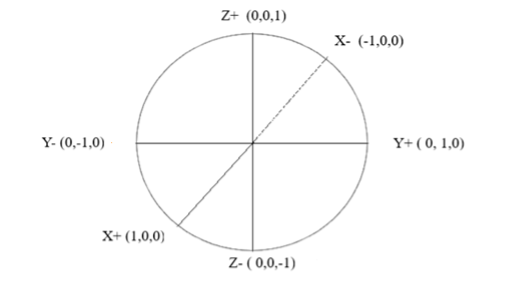
During my study of Quantum theory, I wanted to understand rotation better. I went on-line to see if I could buy a Bloch Sphere or any 3d sphere. I found a t-shirt and loads of dance shoes but no Bloch Spheres. As the government would not allow me to use my tennis balls for tennis, I decided to make my own 3d Sphere I took a Wilson Triniti eco-friendly tennis ball from my dusty sports bag. The only writing on the ball was the Triniti logo, so I used this to represent the North Pole.
- Here with the logo the right around, I wrote Z+ in the centre of the logo and the Cartesian coordinates (0, 0, 1) below.
- On the opposite side, I marked Z- in the centre and (0, 0, -1) below.
By holding the tennis ball at these 2 points between my thumb and big finger, I had made the z-axis. I was able to rotate the tennis ball easily.
- Holding the ball vertically by the z-axis, I then marked in the X+ pole in the centre and (1, 0, 0) on the side facing me and then the X- pole in the centre with (-1, 0, 0) on the opposite side to get the x-axis.
- Continuing to hold the ball at the z-axis points, I turned it 90o counterclockwise or to the left and marked in the Y+ pole in the centre with (0, 1, 0) and then the Y- pole in the centre with (0, -1, 0).
Turning counterclockwise and clockwise on the tennis ball can be confusing as the ball and your viewpoint seem to change. To make sure I was moving correctly I marked the counterclockwise rotation on the ball using the following diagram.
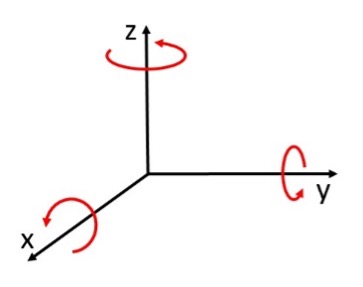
- With Z+ facing me and X+ below, I drew the symbol ⥀ around the Z+ with a second arrow pointing right on the bottom of the ⥀ symbol (Alt 10560). This was to show the direction of the counterclockwise or positive rotation, no matter what angle I held the tennis ball.
- With Y+ facing me and Z+ facing me I drew the symbol ⥀ around the Y+ with a second arrow pointing right on the bottom of the symbol.
- With X+ facing me and Z+ above me I drew the symbol ⥀ around the X+ with a second arrow pointing right on the bottom symbol.
To check that my arrows are correct, I held each axis parallel to the ground with the positive side towards me. Rotation clockwise and counterclockwise around the axis is then in the same direction as for a clock. i.e. The ball moves left during a counterclockwise rotation and right during a clockwise rotation. I then realised that if I was looking at one side of the ball and it was moving left, the other side was moving right. You cannot really use left and right when describing rotation. If I want the ball to rotate counterclockwise, I need to check that it is moving in the direction of the arrows and vice versa for clockwise.
At last, I had a sphere that I could use to understand rotation. It’s not exactly a Bloch Sphere, but it is a good start. Instead of trying to make a mental picture of rotation, I could rotate with the tennis ball. Another thing I had to remember was that whenever I rotated the ball, I had to keep the axes in there standard configuration. In other words X+ facing me, Z+ to the north and Y+ to the east.
The X, Y and Z axes themselves do not move when rotating around them. It is the point in question that rotates. So, by rotating the ball by a quarter turn I could rotate a point located at X^ to Y^. My tennis ball did not reflect this as the X-axis rotated as well. After the quarter turn rotation the X^ has moved to the previous location of the Y^. It should be the point that has moved and not the X. This needs to be taken into account when looking at rotations. To be clear, the axes are fixed and locations are fixed in relation to the axes. Rotation causes a point to move between locations. My tennis ball needs an upgrade. [1] In between rotations it is simplest to record the new location of a point and then return the ball to its standard configuration of X+ facing me, Z+ to the north and Y+ to the east.
Let’s try a rotating a point located at X+.
- Holding the tennis ball by the z-axis with the Z+ at the north pole and X+ facing me, I made a one quarter or 90o turn counterclockwise in the direction of the arrows at Z+.
X+ moved to the previous location of Y+. This needs to be interpreted as the point located at X+ moving to the location Y+. The point located at (1,0,0) had moved to the location (0,1,0). In two-dimensions i is at the location (0, 1).
- I returned the ball to its standard location. One more quarter counterclockwise moved Y+ to the original location of X-. Again this needs to be interpreted as the point at Y+ being moved to the location X- at (-1, 0, 0).
In two-dimensions, the location -1 on the x-axis is at (-1, 0). Two quarter turns counterclockwise had brought me to the three-dimensional equivalent of -1. If one turn brought me to the equivalent of i and two to -1, maybe this is how √-1 = i is determined. This did not seem exactly right, as there was no multiplication involved, just the performance of two rotations. Maybe √-1 = i means that it takes two counterclockwise rotations of i to get from 1 to -1.
[1] I need a prop where the X, Y and Z axes are fixed and an outer transparent sphere could rotate around these axes. Maybe the axes could be fixed by using magnets or by using light for the axes?
locations of i,j and k. I expected i to be at point (0,1,0) on the y-axis the same way as it is at the point (0,1) in two dimensions.
It is well known to mathematicians, but eventually I stumbled on the fact that in three-dimensions in Euclidean Geometry the point (0,1,0) on the y-axis is labelled j. The point (1,0,0) on the x-axis is i and the point (0,0,1) on the z-axis is labelled k.18 Why did they change the labelling?
So I added the label i beside X+ (1,0,0) on the tennis ball prop. I did the same for –i, j, -j, k and –k as in the diagram above.
Let’s now try rotating a point through ijk.
- I held the ball by the y-axis with i facing me. I made one quarter turn of the ball counterclockwise on the y-axis, a turn of j.
The point at k moved to the previous location of i.
- Next, I returned the ball to its standard configuration with Z+ at the north pole. I changed my hold to the x-axis. I made one quarter turn of the ball counterclockwise.
This now left the point at i, but rotated by 90o.
Where was -1? I then realised that there is no -1 on the ball. As described in Quaternions -1 is a scalar in a fourth dimension. Therefore, a 90O turn counterclockwise of Z- resulted in -1. Was this the equivalent of i2 = -1 in Quaternions? Would a 90O turn clockwise result in 1? Maybe this is how it works.
When Hamilton stated ijk = -1, what he meant is that if you start at the point k and apply the rotation j and then i, then you end up at the point -1. Similarly, if you start at -i and rotate by ijk you will end up at 1.
But 1 and -1 are not really on the tennis ball as they are in the ‘4th’ dimension and are really only scalars without a dimension. So how would you expect to rotate and find -1 on the ball when it is in another dimension? The k in ijk indicates the start location of the point is k. The rotation j moves the point from the location k to the location i. The rotation of the point at i by i brings you back to the scalar -1. Of course, i is also the result of applying a rotation of i to the scalar 1.
Eureka, but have I finally understood Quaternion rotations? All it took was the Irish Government to ban tennis.
The one thing I noticed when rotating was that I had the option to rotate either clockwise or counterclockwise. I never did any negative rotations. In fact, the only thing that distinguishes a clockwise to an anti-clockwise movement is the direction. So how had I ended up with negative coordinates?




